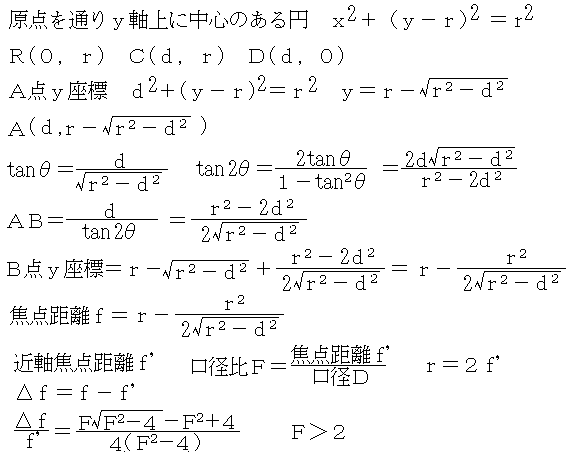
球面反射鏡(20120908)

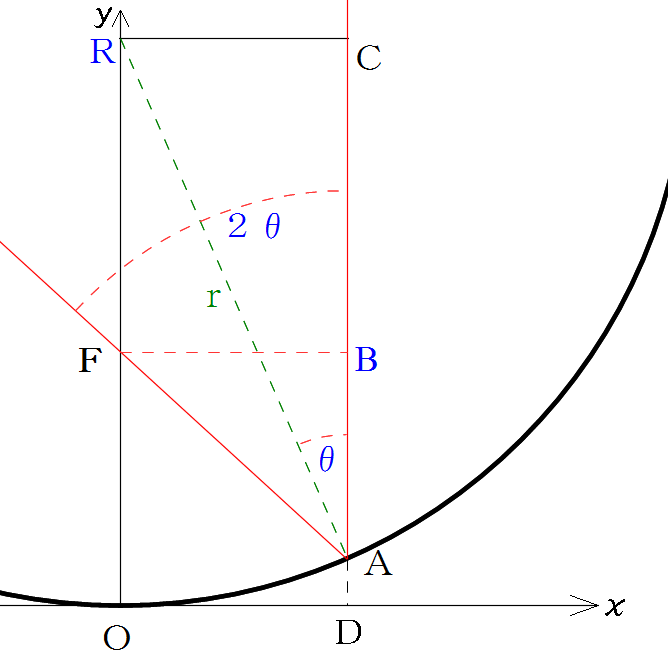
　原点を通り、ｙ軸上に中心のある円をｙ軸で回転させると球面になります。この面の外側（凸面）または内側（凹面）を反射面としたものが球面鏡です。この凹面を使った球面反射鏡を用いて望遠鏡を作ることができます。ここで、問題を簡単にするために、この望遠鏡の光路としてｙ軸を含む任意の方向の平面を考えてみます。ここで、ｙ軸に平行で間隔ｄだけ離れた入射光線ＣＡがどの様に反射していくかを計算します。
　球面鏡の1点Ａに入射した光は、反射します。この時、入射角∠CARと反射角∠RAFが等しいという反射の法則に従います。A点の法線はＡ点から円の中心Ｒを通る直線となることから、任意の入射光についてＦの位置を求めます。

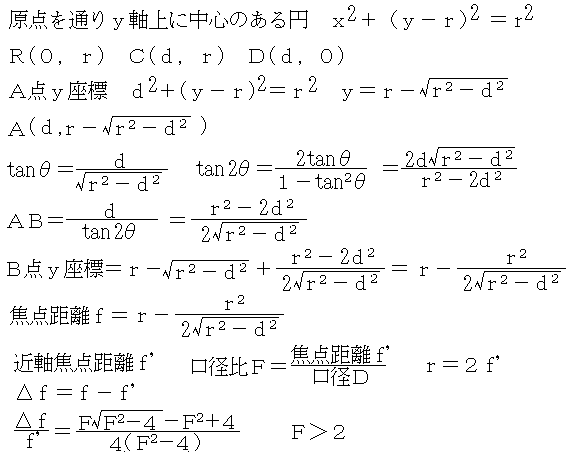
　計算自体は、それほど困難なものではありませんが、三角関数で引っかかりそうな場合は公式集等を手に入れると良いかも知れません。この計算の結果は、中心からｄだけ離れた光線が光軸に反射されて集中しようとした場合に、球面の中心から焦点までの距離（焦点距離）がｄの関数になっていることです。つまり、球面に入射した光は、一点に集中するのでは無く、中心の光軸からの距離によって集中する位置が違うという結果です。そして、式をよく見れば、ｄが小さい場合はｒ／２の位置が焦点距離となることが判ります。軸から離れるにつれ、より球面に近いところに集まるようになるのが球面鏡の性質ということになります。実体の像を作るのが、対物鏡と呼ばれるものの役目ですが、像と実体とが大きさ（倍率）以外の点で違ってきてしまうことを収差と呼びます。１点に集まるべき光が、集まらないのも収差の一つであり、これには球面の収差である事から球面収差と名付けられています。
　焦点位置を出す式の解釈として、ｄがｒに近づけばルートの中がゼロに近づき焦点位置は球面を超えて負の位置へと飛び込みます。当然ですが、ｒはｄ以上にはなれません。ここで、Ｆの位置がｙ軸の正領域にいる条件は入射角・反射角が６０度以下であることが計算から出ます。

　ところで、反射望遠鏡を自作しようとする場合には、後述の放物面鏡を使うのが推奨されています。球面鏡を使用する事は出来ないのでしょうか。計算で確認してみましょう。図中のＯＺラインが、この場合の光軸となり、近軸光線はこの光軸に近いところの光となります。曖昧な表現ですが、収差を無視する方便または指示です。近軸光線、つまりｄがｒに対して小さい値の場合、球面鏡の焦点距離ｆはｒ／２になることを求めた式は示しています。そこで、球面の周縁での焦点距離ｆ’と、理想の焦点距離ｆの差を、理想の焦点距離ｆ’に対する比率を求める計算式を作成すると、口径比Ｆの関数にまとめることができます。

　反射望遠鏡が安価に量産できるようになった背景には、球面鏡であれば簡単に作れるようになったという製造技術の進歩と、放物面ではなく球面鏡でも、スペックに寄れば使えることが判ったという背景があります。これが放物面鏡を作るとなると、１枚１枚、数少ない熟練者による手作業で作られたのですから、量産は不可能なことだったのです。さて、当時のスペックは直径１０センチ、焦点距離１０００ｍｍです。計算はｒ＝１０００×２ｍｍ、ｄ＝５０ｍｍを使います。すると、反射鏡が球面鏡であった場合、外周で反射した光は、誤差０．５％、９９９．６８７・・・・・・mm、つまり、指定の焦点位置から０．３１２６ｍｍ内側で結像します。焦点位置で待っていたら、直前で結像して焦点面では少し広がることになりますが、その広がりは０．０３ｍｍの大きさになります。実際のところ、ニュートン式斜鏡とその支持体を含めた回折の影響を考えれば、この程度の収差であれば実用上充分な性能を出すことが可能だといえます。
　これに対してＦ＝６．０とすると１．５％、Ｆ＝４．０とすると３．９％というように、Ｆ数が明るくなるに従って急速に収差状況は悪化し、球面鏡での性能は落ちることになります。最近の明るめの光学系では、球面鏡では性能を出せないということになりますが、研磨技術も進んでいて、そこそこの放物面であれば、量産可能となっていることから、価格を維持しながらそこそこの性能を持つようになっていると言えるでしょう。