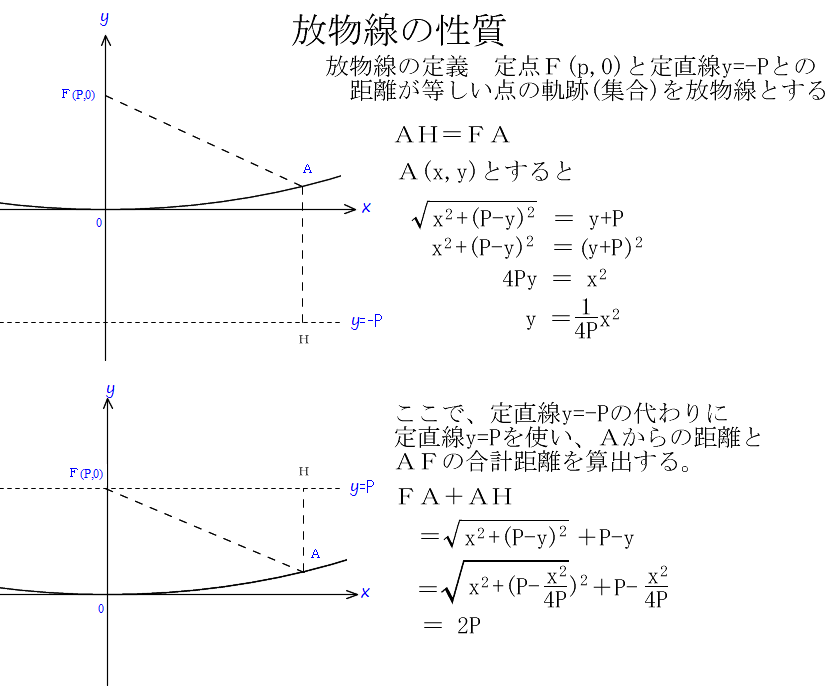
放物面反射鏡(20120909)

放物線は、以上のような性質を持っていますが、放物線の軸方向から来る光線が放物面で反射した場合にどうなるかは、定義には入っていません。そこで、y軸プラスの方向から来る平行光線がどうなるかを調べて見ましょう。
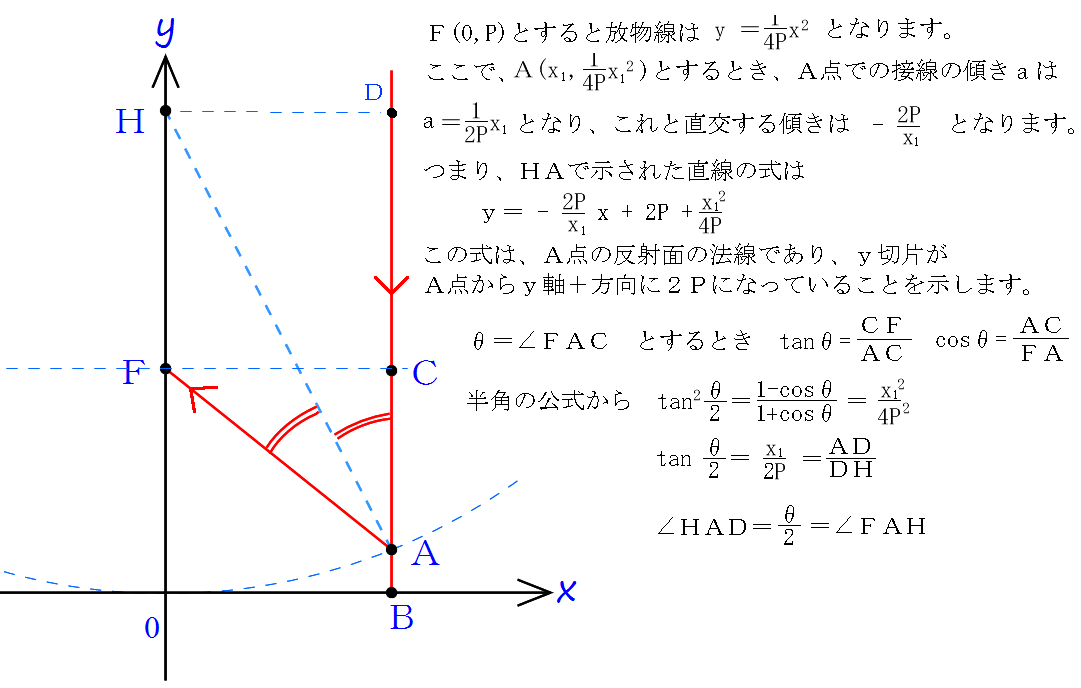
y軸プラス方向から軸に平行に入射する光線は、放物線で反射されると、全て焦点に集まるようになっているのです。これは平面上の話ですが、y軸を回転させてできる回転放物面でも、同じ事が起こります。
軸を増やして、xyz軸とし、xz平面またはyz平面で、原点を通り下に凸の放物線を用意して、z軸を回転させると回転放物面ができます。この放物面鏡は、原理的に光軸に平行な光束を1点に集中させることができます。 先ほどの1点(焦点)に光線が集中するのは、放物面の形状に原因しています。しかし、z軸に対して傾いている光線はどうなるのでしょうか。これを調べて見ましょう。
原点を通る放物面がz軸マイナス方向に凸となっている場合を考えます。放物面の焦点位置はFであり、焦点距離はPとなっています。この状態の時に、斜めの光線BAが入射し、A点で反射、焦点面をDで通過するとします。
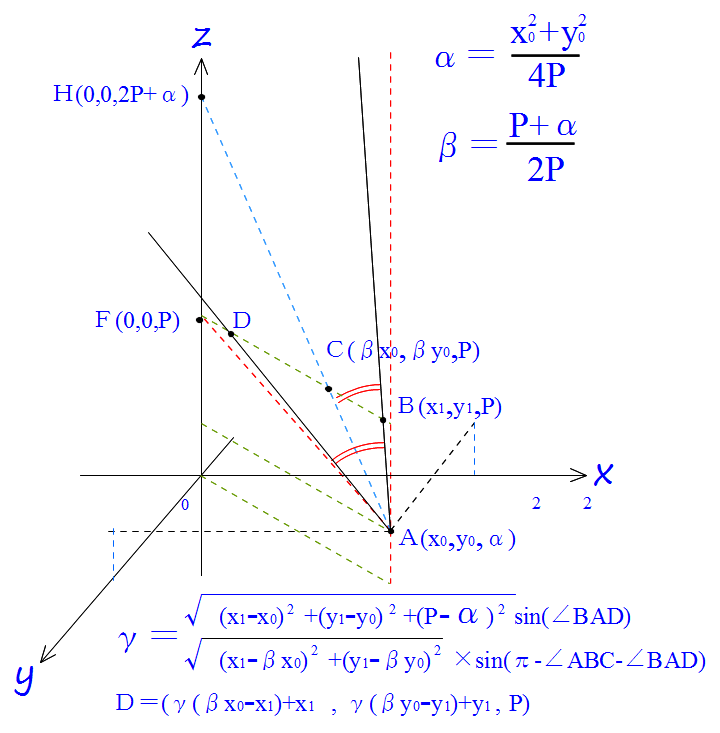
FDCB面 放物面の焦点を含む焦点面
A 放物面上の反射点
B 光線BAが焦点面を通るときの位置
C A点の反射面の法線が焦点面と交わる点
D 反射した光線が焦点面を通るときの位置
H A点の反射面の法線がz軸と交わる位置
DCBは焦点面の中で、一直線の上にあります。ここで三角形△BACと△BADは同一平面上にありますから、通常の三角形の公式を適用することができます。∠BAD=2×∠BACであることから、BCとBDの長さの比を求めることができます。ここから、Dの座標を計算することができます。
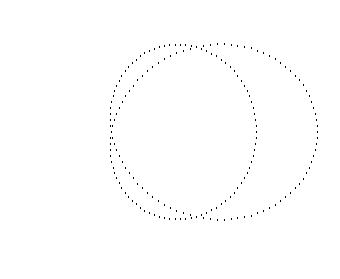 放物面に入る光線の反射点を中心から同距離の円として、斜めの光線を入れると、焦点面を通る光線は図のような形になりました。斜めの光線の斜め具合と、中心からの距離が大きくなると焦点からの誤差が大きくなっていきます。
放物面に入る光線の反射点を中心から同距離の円として、斜めの光線を入れると、焦点面を通る光線は図のような形になりました。斜めの光線の斜め具合と、中心からの距離が大きくなると焦点からの誤差が大きくなっていきます。
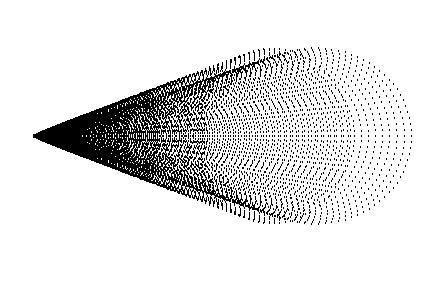 反射面に半径を徐々に大きくしていった円状の光線を入れた場合に出る収差の状況。
反射面に半径を徐々に大きくしていった円状の光線を入れた場合に出る収差の状況。
 反射面に、斜めの角度の同じ光線を格子状に入れてみた場合の収差の状況。
反射面に、斜めの角度の同じ光線を格子状に入れてみた場合の収差の状況。
放物面鏡では、光軸に平行な光は、焦点に集中しますが、斜めになると1点では無く外側にぼやけるようになる収差が出ます。髪の毛がなびくように見えることからコマ収差と名付けられています。反射鏡のF数と斜めの具合に関係したぼやけ方をします。補正レンズを用意する方法もありますが、広角の位置観測に使うには、大変に困る収差で、広視野で明るい光学系を必要とする場合は、放物面鏡1枚では限界があります。
コマ収差による像ののびは0.186×f÷F÷F×tanω[mm] または 0.186×f×D÷F×tanω[mm] f:焦点距離mm F:口径比 ω:光軸からの角度rad D:口径mm で計算できます。
| コマ収差によるイメージサークル(φmm) | ||||
| 口径比 | 星像の伸び(mm) | |||
| 0.005 | 0.010 | 0.050 | 0.100 | |
| 4.0 | 0.43 | 0.85 | 4.27 | 8.53 |
| 4.5 | 0.54 | 1.08 | 5.40 | 10.8 |
| 5.0 | 0.67 | 1.33 | 6.67 | 13.3 |
| 6.0 | 0.96 | 1.92 | 9.60 | 19.2 |
| 8.0 | 1.71 | 3.41 | 17.1 | 34.1 |
| 10.0 | 2.67 | 5.33 | 26.7 | 53.3 |